About Me

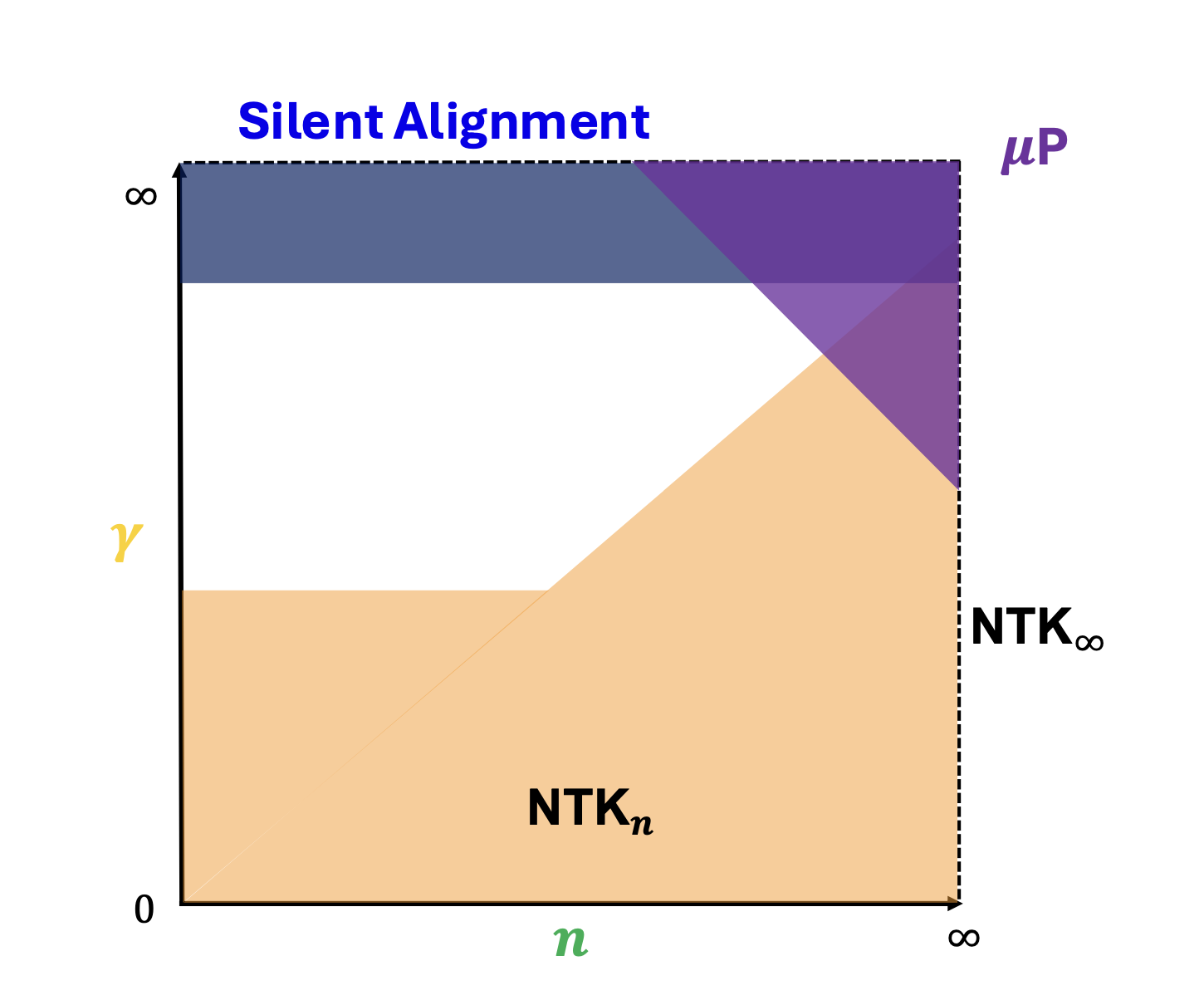
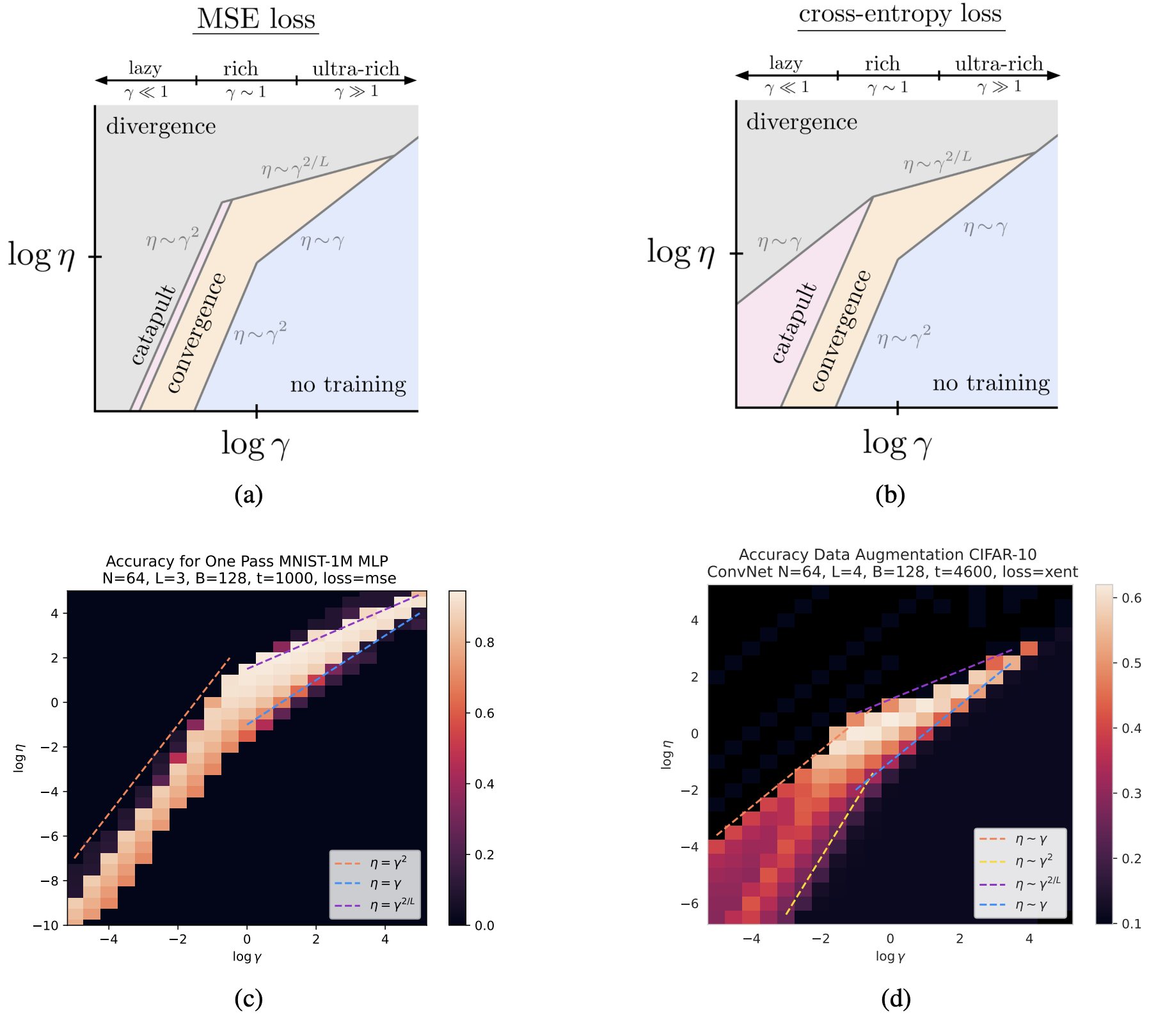
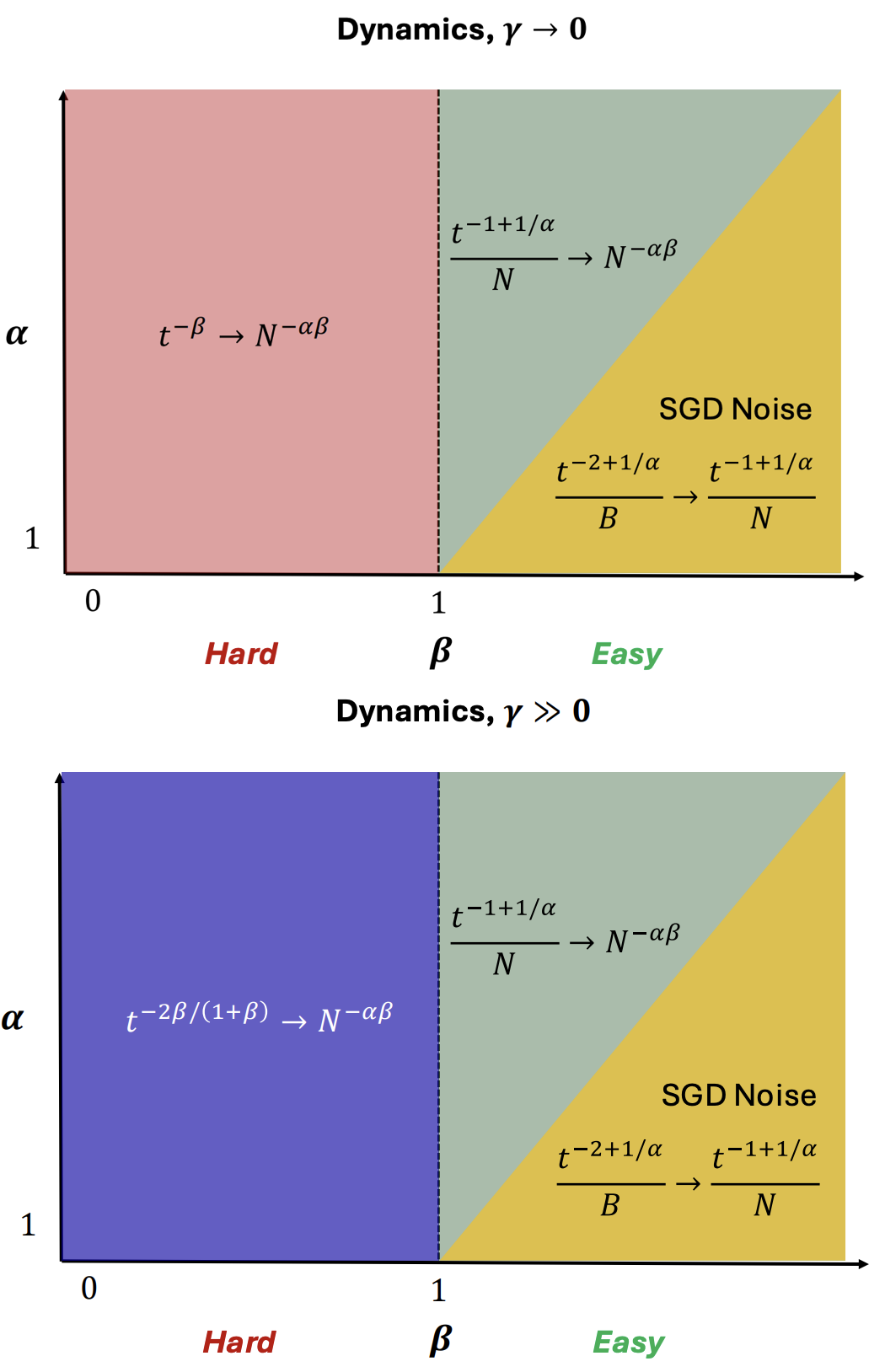
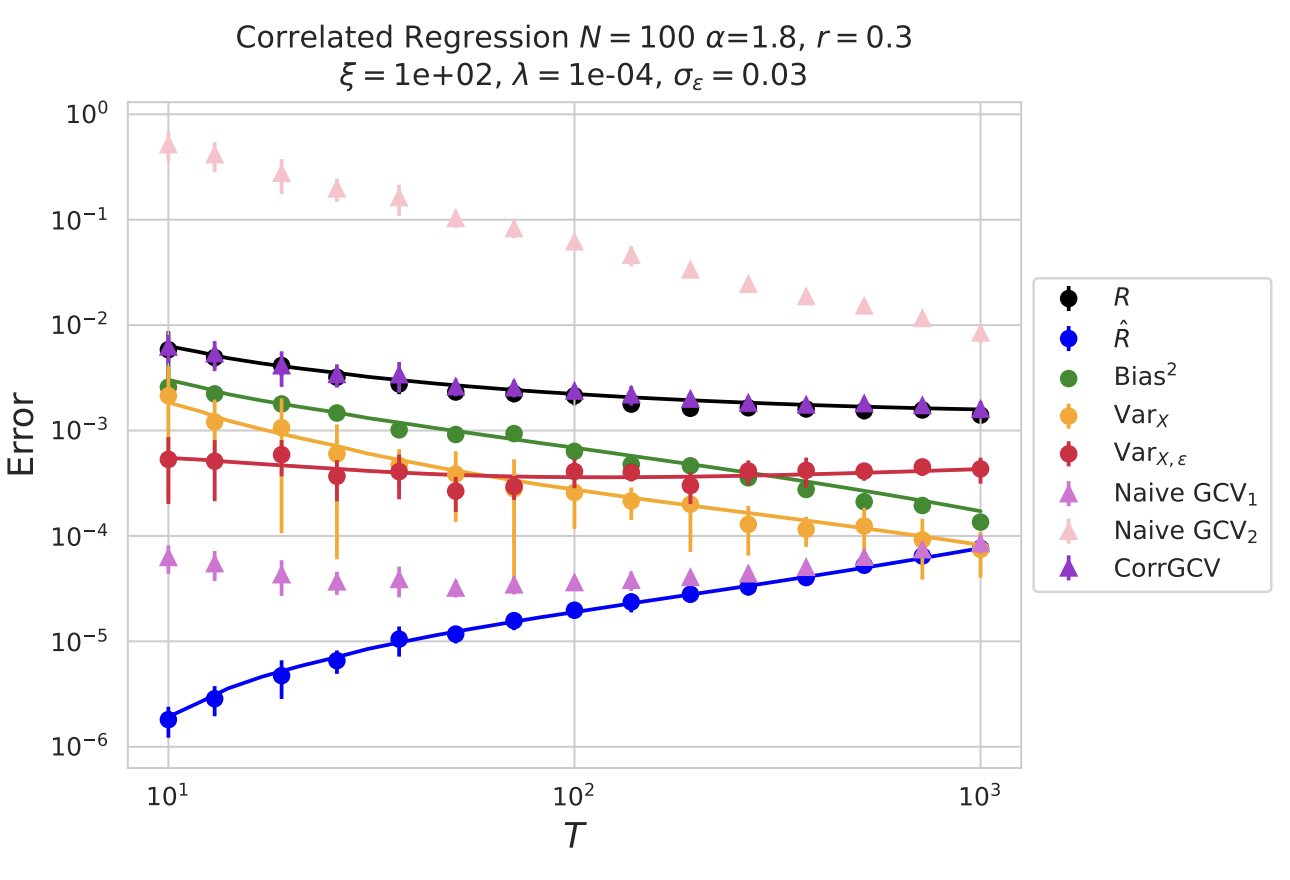
I am a researcher in industry. I recently completed my PhD in theoretical physics at Harvard, where I was very fortunate to be advised by Cengiz Pehlevan. My research is on developing a science of deep learning to inform the design of AI systems that are more performant, reliable, and interpretable. I approach this by leveraging statistical physics, random matrix theory, and extensive empirical studies on real models and datasets. Key ideas include the neural tangent kernel, maximal update parameterization (μP), and the dichotomy between rich and lazy training. An important application of these ideas is to the study of neural scaling laws. See this note for a 2-page derivation of key scaling laws obtained in my PhD. My work was funded by the NDSEG Fellowship (2019-2022) and by the Hertz Fellowship (2019-2024).
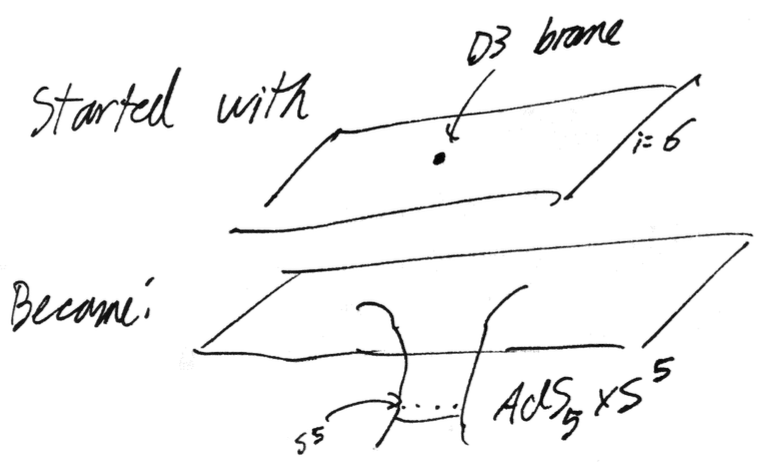
Prior to this, I had the pleasure of collaborating with Andy Strominger and colleagues on topics adjacent to string theory and quantum field theory. Also while in graduate school, I consulted for two biotech firms: Protein Evolution and Quantum Si as a machine learning scientist. I've also worked at Jane Street as a quantiative research intern, at Google applying deep learning to computer vision, and at the Perimeter Institute under Erik Schnetter on tackling the curse of dimensionality in numerical partial differential equations.
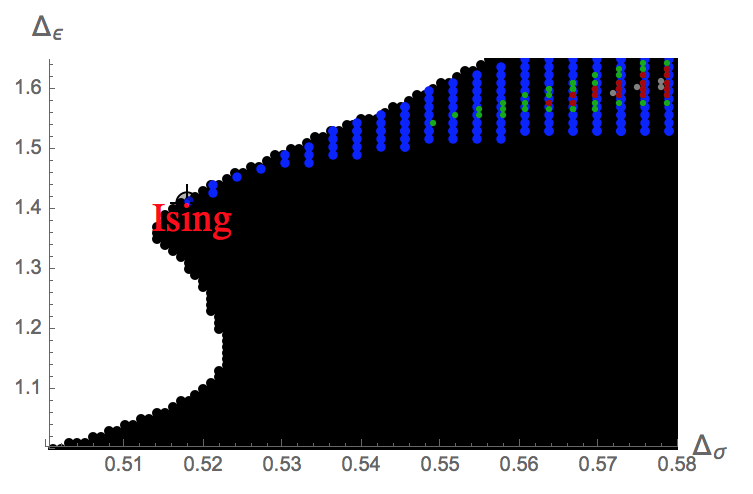
I received my M.S. in mathematics and B.S. in physics from Yale in 2018. There, I studied conformal field theories under David Poland, using the bootstrap program. I also studied computational neuroscience in John Murray's lab, where we built tools to study working memory in recurrent neural networks. My master's thesis in pure math was under Philsang Yoo on connections of quantum field theory to the Langlands program.
My earliest exposure to scientific research was under Dr. James Ellenbogen at MITRE, and with Drs. John Dell and Jonathan Osborne at Thomas Jefferson High School.